井字棋棋盘
Tic-Tac-Toe又称井字棋，即在3X3的棋盘上，双方轮流落子，先将3枚棋子连成一线的一方获得胜利。
Tic-Tac-Toe变化简单，只有765个可能局面，26830个棋局，因此常成为博弈论和游戏树搜寻的教学例子，同时也是人工智能的一道好题目。
关于棋盘：
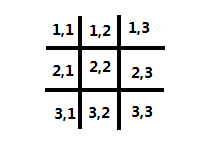井字棋棋盘坐标版
整个棋盘可以连接出8条线。tic-tac-toe 井字棋 胜利方式（如右图）——>
在中心的位置（2，2）有四条线穿过。
在所有棱位（1，2），（2，1），（2，3），（3，2），均有两条线穿过。
在所有角位（1，1），（1，3），（3，1），（3，3），均有三条线。
如何实现人工智能：
在下棋过程中，任何一方无非处于四种状态：
开局落子
第二步棋（先角原则）
攻
守
垃圾时间
想要实现人工智能，让AI和人正常对弈，必须让AI理解这5种状态。
开局落子：
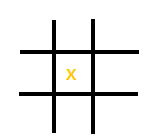井字棋 AI先手[/caption]
开局时，分为两种状况，一是AI先手，二是AI后手。AI先手时，毫无疑问，让AI落子在(2,2)位置（以X表示AI）。如图：
而当AI后手时，玩家可能落子情况有分为三种：
中心位置
棱位
角位
1、玩家落子在中心位置：
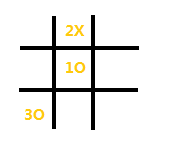图1[/caption]
此时，AI需要落子在角位。原因在于，如果落子在棱位，将出现如下必输的情形，示例如下，AI此时落子在（1，2）位置：玩家只需要在（3，1）或（3，3）位置落子，如图在（3，1），下一步则必须落子在（1，3），对手跟进落子在（1，1），
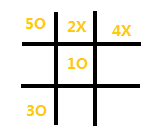——则AI大势已去！
2、棱位 3、角位
这两种情形，AI指需要落子在（2，2）位置，便可保无虞，甚至反守为攻。
第二步棋（先角原则）：
由上可知，当中心被玩家占据，需要避免上边提到的“必输的情形”跟进落子在角上，而非棱上。
而如果，自己占据中心，玩家落子在棱上，根据“必输情形”，此时也应该落在角上，而且如上图图1，应该落子在玩家棋子对面的角位上，此时“必输情形”将属于玩家。
攻：
任何己方两枚棋子连接在一起，且连线有空位时，落子在空位。
守：
任何玩家两枚棋子连接在一起，且连线有空位时，落子在空位。
垃圾时间：
由于棋盘大小限制，下棋过程中，很容易陷入双方均无法获胜的情况，此时，只需要找个空位随便落子即可。
特殊情况：
在以以上方式实现AI时，出现了一种比较特殊情况。即玩家先手，落子在角位以（1，1）为例，AI根据“开局落子”的原则3，落子在（2，2）。而玩家在第一步棋子位置（1，1）的对角（3，3）位置落子，
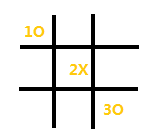井字棋 特殊情况[/caption]
依据“角先原则”，AI将落子在（1，3）或（3，1），对方将在（3，1）或（1，3）封堵AI，此时AI便已输了。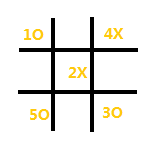
所以，唯有此种情况不能执行“角先原则”。
代码实现：
其中，以二维数组t[3][3]表示棋盘，-1表示AI棋子X，1表示玩家棋子O，
dropPiece(Position p)方法表示落子，Position（int f ,int x,int y）表示棋盘位置，x,y表示坐标值，f取值范围为（-1或1）表示AI或者玩家。下面是AI类主要代码：
public void start(){
if(attrack()){//实现攻
}else if(defend()){//实现守
}else if(center()){//实现开局落子
}else{
planB();//实现特殊情况、先角原则及垃圾时间
}
}//以上方法是AI运行开始的方法
public boolean attrack(){
return twoPieces(-1);
}//攻，任何己方两枚棋子连接在一起，且连线有空位时，落子在空位。
public boolean defend(){
return twoPieces(1);
}//守，任何对方两枚棋子连接在一起，且连线有空位时，落子在空位。
private boolean twoPieces(int f) {
for(int i=0;i<=t.length-1;i++){
if(t[i][0]==t[i][1]&&t[i][0]==f&&t[i][2]==0){
b.dropPiece(new PieceLocation(-1,i,2));return true;
}else if(t[i][0]==t[i][2]&&t[i][0]==f&&t[i][1]==0){
b.dropPiece(new PieceLocation(-1,i,1));return true;
}else if (t[i][1]==t[i][2]&&t[i][1]==f&&t[i][0]==0){
b.dropPiece(new PieceLocation(-1,i,0));return true;
}else if(t[0][i]==t[1][i]&&t[0][i]==f&&t[2][i]==0){
b.dropPiece(new PieceLocation(-1,2,i));return true;
}else if (t[0][i]==t[2][i]&&t[0][i]==f&&t[1][i]==0){
b.dropPiece(new PieceLocation(-1,1,i));return true;
}else if(t[1][i]==t[2][i]&&t[1][i]==f&&t[0][i]==0){
b.dropPiece(new PieceLocation(-1,0,i));return true;
}
}
if (t[0][0]==t[1][1]&&t[0][0]==f&&t[2][2]==0){
b.dropPiece(new PieceLocation(-1,2,2));return true;
}else if(t[1][1]==t[2][2]&&t[1][1]==f&&t[0][0]==0){
b.dropPiece(new PieceLocation(-1,0,0));return true;
}else if(t[0][2]==t[1][1]&&t[0][2]==f&&t[2][0]==0){
b.dropPiece(new PieceLocation(-1,2,0));return true;
}else if (t[1][1]==t[2][0]&&t[1][1]==f&&t[0][2]==0){
b.dropPiece(new PieceLocation(-1,0,2));return true;
}else{
return false;
}
}//包含任何己方两枚棋子连接在一起，且连线有空位的情况
//（横向、纵向和斜着的方向）
public boolean center(){
if(t[1][1]==0){
b.dropPiece(new PieceLocation(-1,1,1));return true;
}else{
return false;
}
}
public void planB(){
if(t[0][0]==t[2][2]&&t[0][0]==1||t[0][2]==t[2][0]&&t[0][2]==1){
if(t[0][2]==0){
b.dropPiece(new PieceLocation(-1,0,2));
}else{
b.dropPiece(new PieceLocation(-1,0,0));
}//特殊情况实现代码
}else if((t[0][1]==1||t[1][2]==1)&&t[2][0]==0){
b.dropPiece(new PieceLocation(-1,2,0));
}else if((t[1][0]==1||t[2][1]==1)&&t[0][2]==0){
b.dropPiece(new PieceLocation(-1,0,2));
//以上四行为先角原则的实现 以下为垃圾时间代码实现，即从座至右，
//从上到下，扫描整个棋盘，然后寻找空位，落子。
}else if(t[0][0]==0){
b.dropPiece(new PieceLocation(-1,0,0));
}else if (t[0][2]==0){
b.dropPiece(new PieceLocation(-1,0,2));
}else if(t[2][0]==0){
b.dropPiece(new PieceLocation(-1,2,0));
}else if (t[2][2]==0){
b.dropPiece(new PieceLocation(-1,2,2));
}else if(t[0][1]==0){
b.dropPiece(new PieceLocation(-1,0,1));
}else if(t[1][0]==0){
b.dropPiece(new PieceLocation(-1,1,0));
}else if(t[1][2]==0){
b.dropPiece(new PieceLocation(-1,1,2));
}else
b.dropPiece(new PieceLocation(-1,2,1));
}
}
The Original Link: http://baham.github.io/08_02_328.html
If you want to reprint it, please do under the CC BY-NC-SA 4.0